Propriedades de triângulos

CEVIANAS E PONTOS NOTÁVEIS DE UM TRIÂNGULO

Em um triângulo, ceviana é qualquer segmento de reta que une um vértice à reta suporte do lado oposto. As principais cevianas são: mediana, bissetriz e altura. Outra linha que também tem propriedades muito importantes e será estudada neste módulo é a mediatriz.

MEDIANA

Mediana é o segmento de reta que une o vértice ao ponto médio do lado oposto.

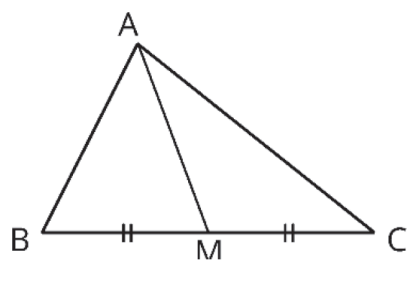
AM é mediana relativa ao lado BC.

Baricentro

Você já ouviu falar em centro de gravidade? O centro de gravidade de um corpo, é o ponto onde pode ser considerada a aplicação da força de gravidade de todo o corpo. Podemos pensar que todo o peso de um objeto se concentra no seu centro de gravidade. Dessa forma, o equilíbrio de qualquer objeto depende da posição desse centro de gravidade. E manter algo em equilíbrio é muito mais importante do que pensamos em um primeiro momento.

Veja a figura abaixo:

Se você estivesse bem perto desse prédio, será que você não se perguntaria como ele não cai? Esse é um dos exemplos da importância do estudo do centro de gravidade de um objeto. Note que essa propriedade é fundamental na engenharia pois torna possível a construção de edifícios com curvaturas visualmente impactantes e curiosas, sem que corram o risco de desabar.

Por enquanto, vamos nos restringir a estudar o centro de gravidade de um triângulo. Aqui vamos sempre chamá-lo de baricentro. Mas onde ele fi ca em um triângulo?

As três medianas do triângulo se cruzam em um ponto chamado baricentro, aqui indicado pela letra G.

A letra G faz referência ao centro de gravidade do triângulo.

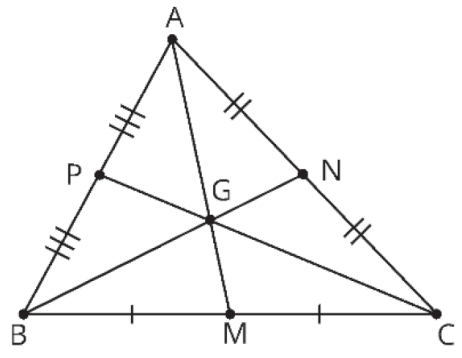
Uma propriedade importante é que o baricentro divide cada mediana na razão de 2 : 1 (Leia-se 2 para 1). Isto é, em cada mediana, a distância do baricentro até o vértice é o dobro da distância do baricentro até o respectivo lado.

Assim, podemos escrever que:

AG = 2 . GM 

BG = 2 . GN 

CG = 2 . GP

Podemos escrever também que:

AG = 2/3 AM e GM = 1/3 AM 

BG = 2/3 BN e GN = 1/3 BN

CG = 2/3 CP e GP = 1/3 CP

OBSERVAÇÃO

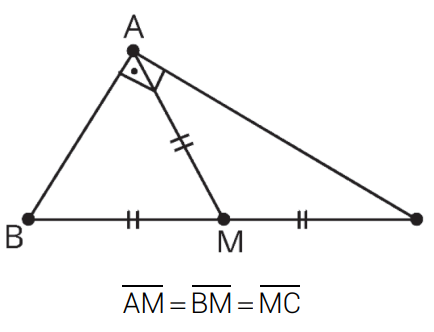
Em um triângulo retângulo, a mediana traçada sobre a hipotenusa mede metade da hipotenusa:

BISSETRIZ

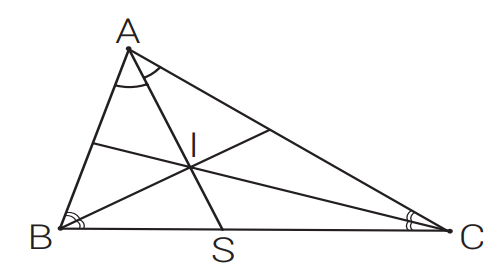
Bissetriz de um ângulo do triângulo é o segmento de reta que divide esse ângulo em duas partes de mesma medida. Na figura, AS é bissetriz do ângulo Â.

EXERCÍCIO RESOLVIDO

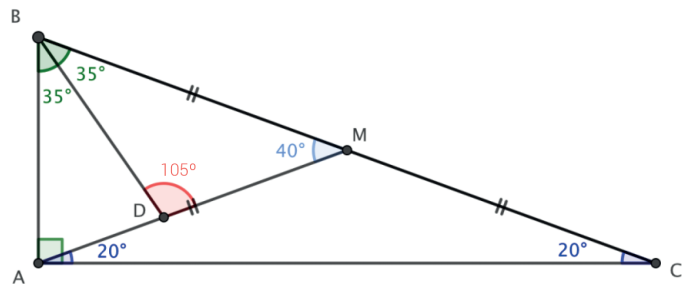
01. Num ∆ABC, retângulo em Â, a mediana AM intersecta a bissetriz interna de B em D. Quanto mede o ângulo BDM, sabendo que C = 20º

Resolução

A mediana AM é congruente aos segmentos MB e MC portanto, o ∆AMC é isósceles. Assim, é fácil concluir que o ângulo MÂC = 20º. Como o ângulo BMD é externo ao triângulo ∆AMC, temos que BMD = 40º. Como B é complemento de C (são ângulos agudos do triângulo retângulo ∆ABC) concluímos que B = 70º e BD é bissetriz do ângulo B o que implica no ângulo DBM = 35º

A soma dos ângulo internos de todo triângulo vale 180º temos portanto o valor do ângulo BDM = 180º – 35º – 40º = 105º.

Use a figura abaixo como suporte:

Incentro

As três bissetrizes internas de um triângulo se cruzam em um ponto chamado Incentro.

OBSERVAÇÃO

• O incentro é o centro do círculo inscrito ao triângulo.

• O incentro é equidistante dos três lados do triângulo. (e essa distância é o raio do círculo inscrito, conforme a figura)

ALTURA

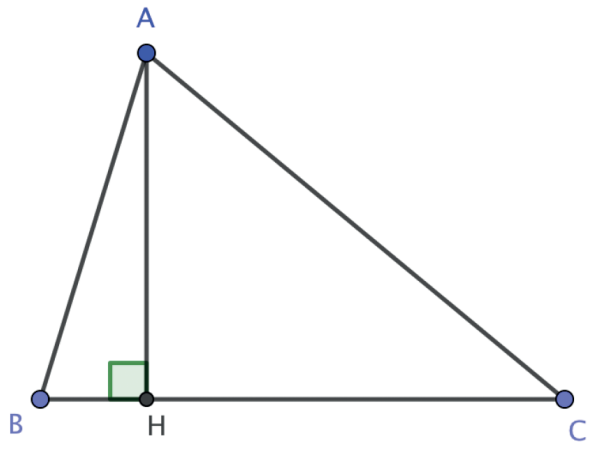
Altura é o segmento de reta que parte de um vértice e é perpendicular à reta suporte do lado oposto. Na figura, AH é a altura relativa ao lado BC.

Ortocentro

As três alturas de um triângulo se cruzam em um ponto chamado Ortocentro. Na figura, o Ortocentro está representado pela letra O.

OBSERVAÇÃO

Em um triângulo retângulo o ortocentro fica exatamente sobre o vértice do ângulo reto.

MEDIATRIZ

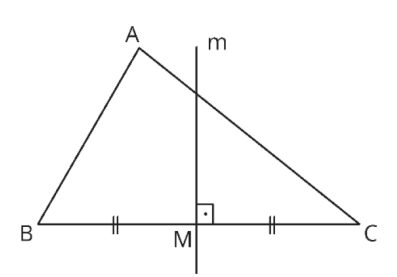
A mediatriz é uma reta que passa pelo ponto médio de um lado do triângulo, formando um ângulo reto com esse lado. Na figura, a reta m é mediatriz relativa ao lado BC.

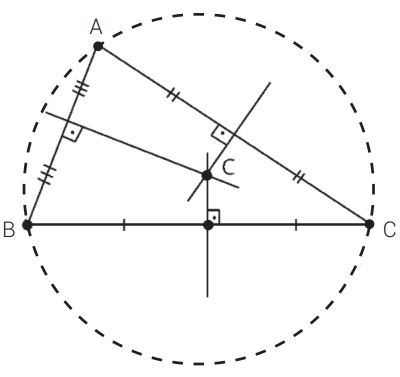
Circuncentro

As três mediatrizes do triângulo se cruzam em um ponto chamado circuncentro. Na figura, o circuncentro está
representado pela letra C.

OBSERVAÇÃO

• Uma observação importante é que o Circuncentro é equidistante dos vértices do triângulo.

• O Circuncentro é o centro do círculo circunscrito ao triângulo.

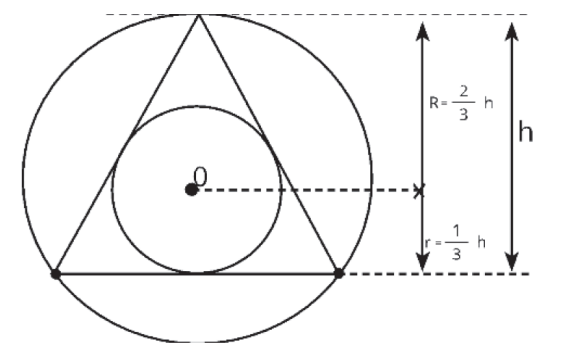
• O centro do triângulo equilátero é ao mesmo tempo baricentro, incentro, ortocentro e circuncentro, isto é, todos esses quatro pontos são coincidentes (estão em um mesmo local). Veja a figura abaixo: