Estude para o Enem totalmente grátis

Progressão Geométrica – Somas

Home » Matemática » Progressão Geométrica – Somas

Progressão Geométrica – Somas

Aprenda sobre a Somar em Progressão Geométrica.

SOMA DOS TERMOS DE UMA PG FINITA

Em uma P.G. não constante (a¹ , a², a³,…an) de razão q ≠ 1, a soma dos n primeiros termos é dada por:

$S_{n}= \frac{a_{1}\cdot (q^{n}-1)}{q-1}$

Demonstração:

Escrevendo a soma dos n primeiros termos, temos:

$S_{}n = a_{}1 + a_{}2 + a_{}3 + .... + a_{n-1 } + a_{}n$

Como $a_{}n = a_{}1 . q^{n-1}$ , substituindo em cada parcela, com o devido cuidado com cada um de seus índices, teremos:

$S_{n}=a_{1}+a_{1}\cdot q^{1}+a_{1}\cdot q^{2}+...+a_{1}\cdot q^{n-2}+a_{1}\cdot q^{n-1} \left ( I \right )$

Multiplicando ambos os membros da igualdade acima pela razão q, teremos

$q \cdot S_{}n = a_{}1 . q^{}1 + a_{}1 \cdot q^{}2 + ... + a_{}1 . q^{n-1 } +a_{}1 \cdot q^{}n \, (II)$

Subtraindo membro a membro, as igualdades (I) e (II), teremos

$q \cdot S_{}n - S_{}n = a_{}1 . q_{}n - a_{}1$
$S_{}n \cdot (q-1) = a_{}1 . (q^{}n - 1)$

Como $q \neq 1$ , dividindo ambos os membros da última igualdade por $q - 1$ , obtemos:
$S_{n}= \frac{a_{1}(q^{n}-1)}{q-1}$

Como queríamos demonstrar.

Observação:

Quando temos a razão q = 1, temos uma P.G. constante. Nesse caso, todos os termos são iguais ao primeiro.

Assim, a P.G. será $(a_{}1, a_{}1, a_{}1, ...)$ . Dessa forma, a soma dos n primeiros termos será dada por $S_{}n = n \cdot a_{}1$

EXERCÍCIOS RESOLVIDOS

01. Calcular a soma dos $12$ primeiros termos da P.G. $(1, 2, 4, ...)$

Resolução:

Temos: $a_{}1 = 1$

$q=2$

Podemos encontrar a soma dos $12$ primeiros termos da P.G., pela fórmula:

$S_{n}= \frac{a_{1}(q^{n}-1)}{q-1}$
$S_{12}= \frac{a_{1}(2^{12}-1)}{2-1}=4905$

02. Calcule a soma dos $10$ primeiros termos da sequência $(3, 3, 3, 3, ...)$

Resolução:

Primeiramente é importante notar que essa sequência pode ser vista como uma P.A. de razão 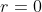$r=0$ , ou ser vista como uma P.G. de razão $q=1$ .

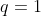De qualquer forma, como acabamos de comentar anteriormente, teremos:

$S_{}n = n \cdot a_{}1$
$S_{}n = 10 \cdot 3$
$S_{}n = 30$

Observação:

Note que, não precisamos de fórmula para resolver o exercício anterior. Basta notar que na sequência todos os termos são iguais a 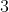$3$ . Como queremos a soma dos 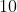$10$ primeiros termos, queremos $10 \cdot 3 = 30$ .

03. Os frutos de uma árvore apodrecem segundo uma progressão geométrica de primeiro termo 1 e razão 3, ou seja, no primeiro dia apodrece um fruto, no segundo dia 3, no terceiro 9 e assim sucessivamente. Quantos frutos apodrecerão ao final de 7 dias?

Resolução:

Temos a PG (1, 3, 9, …, a⁷ ), com a¹ = 1 e q=3.
Podemos encontrar a soma dos 7 primeiros termos da PG, pela fórmula:

Sn= a¹. (qn – 1) / q – 1

S⁷ = 1 . (3⁷ – 1 ) / 3 – 1 = 1093

SOMA DOS TERMOS DE UMA P.G. INFINITA

Em uma P.G. infinita, de razão q, de modo que –1 < q < 1, a soma de seus termos será

$S_{\infty }= \frac{a_{1}}{1-q}$

Demonstração:

Escrevendo a soma infinita (S∞) de uma PG (a1, a2, a3, a4…) de razão q, com -1< q < 1, temos:
S∞ = a1 + a1 q + a1 q2 + a1 q3 +… (I)

Multiplicando ambos os membros da igualdade acima pela razão q, teremos:

q · S∞ = a1 q + a1 q² + a1 q3 + a1 q4 +… (II)

Subtraindo, membro a membro, as igualdades (I) e (II):
S∞ – q · S∞ = a1

Agora fatorando o primeiro membro, pode-se concluir que:
S∞ (1 – q) = a1

S∞ = a¹ / 1 -q

Progressão Geométrica – Somas

Progressão Geométrica – Somas

SOMA DOS TERMOS DE UMA PG FINITA

Observação:

Quando temos a razão q = 1, temos uma P.G. constante. Nesse caso, todos os termos são iguais ao primeiro.

Assim, a P.G. será . Dessa forma, a soma dos n primeiros termos será dada por

Resolução:

Primeiramente é importante notar que essa sequência pode ser vista como uma P.A. de razão , ou ser vista como uma P.G. de razão .

Observação:

Note que, não precisamos de fórmula para resolver o exercício anterior. Basta notar que na sequência todos os termos são iguais a . Como queremos a soma dos primeiros termos, queremos .

SOMA DOS TERMOS DE UMA P.G. INFINITA

Quer aquele empurrãozinho a mais para seu sucesso?

Assim, a P.G. será $(a_{}1, a_{}1, a_{}1, ...)$ . Dessa forma, a soma dos n primeiros termos será dada por $S_{}n = n \cdot a_{}1$

Primeiramente é importante notar que essa sequência pode ser vista como uma P.A. de razão $r=0$ , ou ser vista como uma P.G. de razão $q=1$ .

Note que, não precisamos de fórmula para resolver o exercício anterior. Basta notar que na sequência todos os termos são iguais a $3$ . Como queremos a soma dos $10$ primeiros termos, queremos $10 \cdot 3 = 30$ .