Geometria Espacial – Sólidos Inscritos e Circunscritos
Estudamos até este momento os sólidos separadamente, mas em diversas situações precisamos entender a relação que um sólido tem com o outro. Nesta seção veremos uma relação de inscrição e circunscrição entre dois sólidos.

CILINDRO E PRISMA
Quando o cilindro circular reto está inscrito em um prisma regular, o raio da base do cilindro é o raio da circunferência inscrita na base do prisma, ou seja, o raio da base do cilindro é o apótema da base do prisma. Veja abaixo como exemplo, um cilindro inscrito em um prisma hexagonal regular:

Quando o prisma regular está inscrito em um cilindro circular reto. O raio da base do cilindro é o raio da circunferência circunscrita à base do prisma. Veja abaixo como exemplo, um cilindro circunscrito a um prisma hexagonal regular:

PIRÂMIDE E CONE
Quando uma pirâmide regular está inscrita num cone circular reto, o raio da base do cone é o raio da circunferência circunscrita à base da pirâmide.

Quando um cone circular reto está inscrito numa pirâmide regular, o raio da base do cone é o apótema da base da pirâmide e a geratriz do cone é o apótema da pirâmide.

ESFERA E CUBO
Quando uma esfera está inscrita em um cubo, o diâmetro da esfera possui a mesma medida da aresta do cubo.

Dessa maneira, temos que 2r = a r = a/2.
Quando uma esfera está circunscrita ao cubo, seu diâmetro possui mesma medida da diagonal do cubo.

Dessa maneira, temos que:
2R = a
R = a
/2
Exercícios resolvidos
01. Determine o volume de uma esfera circunscrita a um cubo de 8 cm de aresta.
Resolução:
Como a esfera está circunscrita ao cubo temos que 2R = a.
Dessa forma, .
Para calcular o volume dessa esfera basta aplicarmos a sua fórmula:
02. Determine o volume de uma esfera inscrita num cubo de aresta 6 cm.
Resolução:
Como a esfera está inscrita no cubo temos que 2R = a.
Dessa forma,
Para calcular o volume dessa esfera basta aplicarmos a sua fórmula:
Vᵉˢᶠᵉʳᵃ = 4/3 π.27 = 36πcm³
ESFERA E CILINDRO
Se uma esfera se encontra inscrita em um cilindro circular reto, temos que a altura desse cilindro deve ser o diâmetro da esfera, e o raio da base do cilindro possui mesma medida que o raio da esfera.
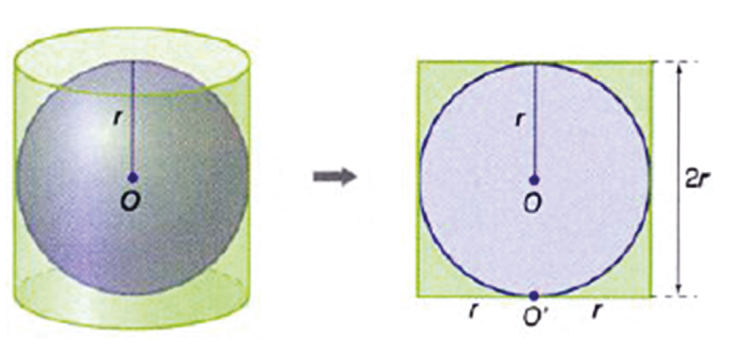
Devemos observar ainda que este, é um cilindro equilátero e que a medida de sua área lateral é a mesma da área da superfície esférica (Alat.cilindro = Aesfera = 4pR2).
Se uma esfera se encontra circunscrita em um cilindro circular reto, temos que o diâmetro da esfera é a diagonal da seção meridiana do cilindro.

Exercício resolvido
03. Determine o volume de uma esfera inscrita num cilindro de volume 54π cm3.
Resolução:
Note que quando uma esfera está inscrita num cilindro temos:
Dessa forma, podemos escrever o volume do cilindro como:
Calculando o volume da esfera, temos:
Vᵉˢᶠᵉʳᵃ = 4/3 π.27 = 36πcm³
ESFERA E CONE
Se uma esferas e encontra inscrita em um cone, temos uma semelhança de triângulos na seção meridiana do cone.

Considere a seção meridiana acima, onde A é o vértice do cone, O é o centro da esfera de raio r, B o centro da base do cone de raio R, e D a interseção da geratriz AC com a esfera. Note que o triângulo ABC é semelhante ao triângulo AOD, assim R/r = g/h
Quando uma esfera está circunscrita a um cone, notemos que o diâmetro da esfera que contém o vértice do cone forma um triângulo retângulo com qualquer dos pontos da base do cone, como mostra a figura.
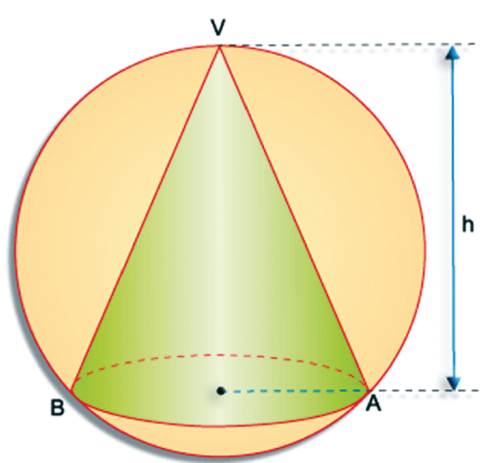

Dessa maneira, considere o triângulo retângulo VV’A, cuja altura relativa à hipotenusa possui a mesma medida do raio r da base do cone, e cujas projeções ortogonais dos catetos sobre a hipotenusa possuem medida h e 2R – h. Logo, pelas relações métricas no triângulo retângulo, temos que:
r2 = h(2R – h).




