Geometria Analítica – Introdução
Aprenda mais sobre Geometria Analítica.

PONTO MÉDIO DE UM SEGMENTO
![]()
Assim, podemos dizer que para qualquer dois pontos A(xᴬ , yᴬ ) e B(xᴮ, yᴮ), o ponto médio M(xᴹ, yᴹ) do segmento AB é dado por:
Xᴹ = Xᴬ + Xᴮ/2 e yᴹ = yᴬ + yᴮ/2
EXERCÍCIO RESOLVIDO
01 . Achar as coordenadas do ponto médio do segmento , sendo A(2, 5) e B(4,-3).
Resolução:
DIVISÃO DE UM SEGMENTO EM UMA RAZÃO DADA
Se um ponto C pertence a um segmento AB e C é distinto de A e de B, dizemos que C divide o segmento AB na razão .

Supondo que AB não é paralelo ao eixo Ox, sendo Xa, Xc e Xb as abscissas de A, C e B, respectivamente, e Ya, Yc, Yb as ordenadas de A, C e B, respectivamente, temos pela semelhança dos triângulos TAC e RCB que:
Baricentro é o ponto de encontro das medianas de um triângulo.
BARICENTRO DE UM TRIÂNGULO

Assim, podemos dizer que para qualquer três pontos A(xᴬ , yᴬ ), B(xᴮ, yᴮ) e C(xᶜ, yᶜ) vértices de um triângulo, o baricentro G(xᴳ, yᴳ) desse triângulo é dado por
Xᴳ = Xᴬ + Xᴮ + Xᶜ /3 e yᴳ = yᴬ + yᴮ + yᶜ
Exercício Resolvido
02. Determine o baricentro do triângulo A (2, 5) , B (–1, 0) e C (5, –2).
Resolução:
DISTÂNCIA ENTRE DOIS PONTOS
Situação 1

Você saberia responder qual é a distância entre os pontos A e B? E entre os pontos C e D?
É possível observar que a distância de A e B são de 4 unidades, que seria o comprimento no segmento AB. Tal distância pode ser calculada como o módulo da diferença entre as abscissas de A e B, isto é, AB = | 6 – 2 |
ou AB = | 2 – 6 |, ou simplesmente, a abscissa maior menos a menor, AB = 6 – 2 = 4.
De maneiro análoga, a distância entre os pontos C e D, pode ser calculada da seguinte maneira: CD = | 4 – (- 2) | = 6
Para calcularmos a distância entre os pontos A e B basta calcular o módulo do vetor ou simplesmente ter a visão analítica e fazer a distância entre dois pontos.
Situação 2
Para calcular tal distância entre A e B, podemos aplicar o Teorema de Pitágoras. Veja abaixo:

Assim, podemos dizer que a distância entre qualquer dois pontos A(xᴬ , yᴬ) e B(xᴮ, yᴮ) é dado por:
d² = (xᴮ – xᴬ)² + (yᴮ – yᴬ)²
d = √(xᴮ – xᴬ)² + (yᴮ – yᴬ)²
Exercício resolvido
03. Determine a distância entre os pontos A(-1,4) e B(3,7).
Resolução:
Utilizando vetores podemos determinar o vetor e calcular o seu módulo.
Logo, a distância entre os pontos A e B é igual a 5.
Ou simplesmente podemos utilizar a relação:
CONDIÇÃO DE ALINHAMENTO DE 3 PONTOS
Os pontos A(xA,yA), B(xB,yB) e C(xC,yC) estarão alinhados se, e somente se:
ÁREA DO TRIÂNGULO
Caso três pontos não estejam alinhados, com certeza estarão formando um triângulo cuja área pode ser calculada por:

ÁLGEBRA LINEAR
SEGMENTO ORIENTADO
O segmento de reta orientado de origem em A e extremidade em B, será representado por e geometricamente representado por:

Caracterizado pelo sentido do segmento.
A distância de A até B (comprimento do segmento) é chamado de módulo do segmento orientado e representado por |.
A direção de é a direção da reta suporte do segmento, e o seu sentido é representado pela flecha (
, de A para B).
SEGMENTOS ORIENTADO EQUIPOLENTES
Se dois ou mais segmentos orientados têm o mesmo módulo, a mesma direção e o mesmo sentido, serão ditos segmentos equipolentes.
VETOR
Vetor determinado por um segmento orientado
é o conjunto de todos os segmentos orientados do espaço que são equipolentes ao segmento
.

Logo, podemos afirmar que é o vetor
aplicado em A,
é o vetor
aplicado em C etc.
Componentes de um vetor no plano (IR2)

Exemplo:
A(3,-1) e B(0,3), se , então:
Representação de um vetor no plano

OBSERVAÇÃO
A projeção de qualquer dos segmentos orientados acima no eixo x é –3, e no eixo y é 1, logo todos os segmentos acima representam o vetor  . Porém, em geral, procuramos marcar um vetor no plano cartesiano aplicando-o na origem, pois assim marcamos apenas o ponto representado pelo par do vetor.
. Porém, em geral, procuramos marcar um vetor no plano cartesiano aplicando-o na origem, pois assim marcamos apenas o ponto representado pelo par do vetor.

Analogamente, tudo que foi visto acima vale para o ℝ3.
Módulo (Norma) de um vetor
O módulo ou norma de um vetor, como vimos anteriormente, é o comprimento do segmento orientado que representa o vetor.
Se então
Exercícios resolvidos
04. Determine o módulo do vetor = (3, 2).
Resolução:
Logo
Logo, se , podemos concluir que
05. (definição análoga para o IR3).
Determine o módulo do vetor .
Resolução:
Propriedades:
•
•
Vetor unitário
O vetor é dito unitário quando .
OBSERVAÇÃO
Dado um vetor 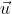 , não nulo, o vetor
, não nulo, o vetor  é um vetor unitário de mesma direção e sentido de
é um vetor unitário de mesma direção e sentido de 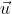 . Esse vetor é denominado versor de
. Esse vetor é denominado versor de 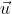 .
.
Exercício resolvido
06. Determine o versor do vetor
Resolução:




