Escalonamento e regra de Cramer
Aprenda sobre Escalonamento e sobre a Regra de Cramer.

PROCESSOS PARA ESCALONAMENTO DE UM SISTEMA LINEAR
Para escalonar um sistema linear, resolvê-lo e depois classificá-lo, alguns procedimentos podem ser feitos:
• T1: um sistema de equações não se altera, quando permutamos as posições de duas equações quaisquer do sistema.
• T2: um sistema de equações não se altera, quando multiplicamos ambos os membros de qualquer uma das equações do sistema, por um número real não nulo.
• T3: um sistema de equações lineares não se altera, quando substituímos uma equação qualquer por outra obtida a partir da adição membro a membro desta equação, com outra na qual foi aplicada a transformação T2.
OBSERVAÇÃO
• Se no processo de escalonamento, obtivermos uma equação com todos os coeficientes nulos e o termo independente diferente de zero, esta equação é suficiente para se afirmar que o sistema é impossível, isto é, tem S = ø.
• Se no processo de escalonamento, obtivermos uma equação com todos os coeficientes nulos e o termo independente igual a zero, esta equação poderá ser eliminada. E todos os termos de números reais são soluções, ou seja, sistema indeterminado.
Agora, para escalonarmos um sistema, deve-se seguir um passo a passo, todos eles relacionados com os procedimentos T1, T2 e T3.
1° passo: A primeira equação precisa estar com o coeficiente da 1ª incógnita diferente de zero. Tente colocar o coeficiente igual a 1, se possível.
2° passo: Nesse processo é necessário anular o coeficiente da 1ª incógnita de todas as equações abaixo da primeira equação (a partir da segunda equação, substitua a linha escolhida pela soma da mesma com a 1ª equação multiplicada por um número conveniente para que anule a linha escolhida).
3º passo: Deixe de lado a 1ª equação e aplique as ideias do 1º e 2º passos nas equações restantes.
4º passo: Agora deixe de lado a 1ª e a 2ª equação e novamente aplique as ideias do 1º e 2º passos nas equações restantes. E assim por diante, até que todo o sistema esteja escalonado. Os exemplos a seguir esclarecerão os passos listados acima.
EXERCÍCIO RESOLVIDO
01. Resolva o sistema abaixo usando o escalonamento.
x + 3y – 2z = 3 (Equação 1)
2x – y + z = 12 (Equação 2)
4x + 3y – 5z = 6 (Equação 3)
Resolução:
{ x + 3y – 2z = 3
{ 2x – y + z = 12
{ 4x + 3y – 5z = 6
1º Tentar colocar o coeficiente do x na 1ª equação, igual a 1.
2º Multiplicar a 1ª equação pelo simétrico do coeficiente x das 2ª e 3ª equações e somar respectivamente.
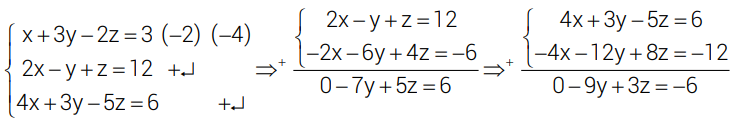
3º Vamos montar o novo sistema com a 1ª equação original e as 2 novas.
{ x + 3y – 2z = 3
{ -7y + 5z = 6
{ -9y + 3y = -6
4º Vamos fazer um sistema com as 2 novas.

5º Temos então:
{ x + 3y – 2z = 3
{ -7y + 5z = 6
{ -24z = -96
6° Usando a última, temos:
-24z = -96 ⟹ z = -96/-24
z = 4
7° Vamos usar o z = 4 na 2ᵃ equação e determinar o y.
-7y + 5(4) = 6 ⟹ -7y + 20 = 6 ⟹ -7y = -14
y = 2
8° Usando z = 4 e y = 2, vamos determinar o x na 1° equação:
x + 3(2) – 2(4) = 3 ⟹ x + 6 – 8 = 3 ⟹ x – 2 + 3
x = 5
S = (5, 2, 4)
02. (UNESP) Os gráficos indicam a diversificação de aplicações para um investimento, por grau de risco, sugeridas por cada um dos bancos A, B e C.

Um investidor decidiu aplicar um capital de R$ 6.000,00 em partes que foram distribuídas pelos três bancos, seguindo a diversificação do grau de risco sugerida por cada banco. O capital aplicado foi distribuído da seguinte forma:
• total de R$ 1.000,00 no banco A (considerando os três graus de risco juntos);
• R$ 2.700,00 em investimentos de baixo risco (nos três bancos juntos);
• R$ 1.850,00 em investimentos de médio risco (nos três bancos juntos);
• R$ 1450,00 em investimentos de alto risco (nos três bancos juntos).
O gráfico a seguir representa a diversificação da aplicação, por grau de risco, juntando os três bancos.

Resolução:
Sabendo-se que foi investido R$ 1.000,00 no banco A seguindo a diversificação do grau de risco apresentada no gráfico, pode-se escrever:
Banco A:
• baixo risco: 80% → 1000 · 0,8 = R$ 800,00
• médio risco: 15% → 1000 · 0,15 = R$ 150,00
• alto risco: 5% → 1000 · 0,05 = R$ 50,00
Sabe-se ainda que foram aplicados:
• R$ 2.700,00 em investimentos de baixo risco, sendo 80% no banco A (correspondente a R$ 800,00), 20% no banco B e 50% no banco C;
• R$ 1.850,00 em investimentos de médio risco, sendo 15% no banco A (correspondente a R$ 150,00,) 70% no banco B e 10% no banco C;
• R$ 1.450,00 em investimentos de alto risco, sendo 5% no banco A (correspondente a R$ 50,00), 10% no banco B e 40% no banco C.
Sendo B e C o montante aplicado em cada um dos bancos, respectivamente, e com as demais informações do enunciado, pode-se escrever o seguinte sistema:

0,6B = 1200 → B = 2000
0,8 . 2000 + 0,5C = 3100 → 0,5C = 1500 → C = 3000
Assim, os montantes aplicados em cada banco foram de R$ 1.000,00 no banco A, R$ 2.000,00 no banco B e R$ 3.000,00 no banco C.
Para calcular os ângulos α, β e γ, indicados no gráfico pode-se utilizar a regra de três:
Baixo risco Médio Risco Alto Risco
6000 ______ 360° 6000____360° 6000____360°
2700______ β 1850____γ 1450____ α
β = 2700.360/6000 → β = 162°
γ = 1850.360/6000 → γ = 111°
α = 1450.360/6000 → α = 87°
03. (UFSC) Se a terna (a, b, c) é solução do sistema { x + 2y + z = 9 ,então calcule o valor numérico de (a + b + c).
{ 2x + y – z = 3
{ 3x – y – 2z = -4
Resolução:
Tomando a matriz ampliada do sistema e escalonando, obtemos

Portanto, o sistema escalonado equivalente é
{ x + 2y + z = 9
{ – y + z = -1
{ -6z = -12
Resolvendo esse sistema, obtemos facilmente x = 1, y = 3 e z = 2. Portanto, segue que a + b + c = 1 + 3 + 2 = 6.
REGRA DE CRAMER
Considerando um sistema linear com o número do incógnitas igual ao número de equações, iremos estudar melhor a regra de Cramer para a resolução de uma sistema linear, baseado do cálculo de determinantes.
Gabriel Cramer (1702-1752) foi um matemático suíço que demonstrou em 1750 a resolução por meio dessa regra, que ficou registrada com o seu nome. E acredita-se que ele não tenha sido o primeiro matemático a fazê-lo, pois os cálculos já eram conhecidos por Maclaurin desde 1729.
CASO 2X2
Inicialmente vamos verificar o uso da regra de Cramer para o caso de um sistema 2×2.
Considerando o sistema de incógnitas x e y:
{ ax + by = p
{ cx + dy = q
Seja M a matriz composta pelos coeficientes do sistema.
Assim, temos que o determinante de M é:
M = [a b] e D = det(M) = ad – bc
[c b]
Se D ≠ 0 , então o sistema é possível e determinado (SPD) e a sua solução (x,y) é dada por:
x = Dˣ/D e y = Dʸ/D
em que Dˣ e Dʸ são os determinantes das matrizes obtidas a partir da matriz M, substituindo a primeira e a segunda coluna, respectivamente, pela coluna dos coeficientes independentes das equações do sistema.
Observe o exemplo:
Utilizando a regra de Cramer, vamos encontrar a solução desse sistema:
{ 4x – y = 18
{ 6x + 4y = 38
Observe que
D = |4 – 1| = 16 – (- 6) 22 ≠ 0,
|6 4|
logo podemos de fato utilizar a regra de Cramer.
Assim, podemos assumir que este sistema é possível e determinado.
Agora vamos calcular os valores de Dˣ e Dʸ
Dˣ = |18 -1| = 72 + 38 = 110
|38 4|
Dˣ = |4 18| = 152 – 108 = 44
|6 18|
Então, os valores de x e y são:
x = Dˣ /D = 110/22 = 5
y = Dˣ/D = 44/22 = 2
Assim, temos a solução do sistema S = {(5,2)}.
CASO 3X3
Agora vamos verificar o uso da regra de Cramer para o caso de um sistema 3×3.
Considerando o sistema de incógnitas x , y e z:
{ ax + by + cz = p
{ dx + ey + fz = q
{ gx + hy + iz = r
Seja M a matriz composta pelos coeficientes do sistema.
Assim, temos que o determinante de M é:
[a b c]
M = [ d e f]
[ g h i]
Se o det (M) = D for diferente de zero (D ≠ 0), temos que o sistema é possível de determinado. E podemos assim utilizar a regra de Cramer para encontrar a solução do sistema.
Assim, a solução (x, y, z) pode ser calculada por:
x = Dˣ/D , y = Dʸ/D e z = Dᶻ/D
em que Dˣ , Dʸ e Dᶻ são os determinantes das matrizes obtidas a partir da matriz M, substituindo a colunas dos coeficientes x, y e z, respectivamente, pela coluna dos coeficientes independentes das equações do sistema.
Observe o exemplo abaixo:
Vamos verificar se é possível utilizar a regra de Cramer, e encontrar a solução desse sistema:
{ x + y + z = 0
{ 2x – y + 3z = -9
{ x – 3y – z = – 2
Primeiramente, vamos calcular o determinante D da matriz incompleta do sistema:
|1 1 1|
D = |2 -1 3| = 10
| 1 – 3 – 1 |
Como D ≠ 0, o sistema é possível e determinado e a sua solução é dada por (x, y, z) que vamos calcular utilizando a regra de Cramer.
x = Dˣ/D , y = Dʸ/D e z = Dᶻ/D
Calculando o valor de Dx, Dy e Dz, temos:
|0 1 1 |
Dx = |-9 -1 3| = 10
|-2 -3 -1|
|1 1 0|
Dz = |2 – 1 – 9| = -30
|1 -3 -2|
|1 0 1|
Dy = |2 -9 3| = 20
|1 -2 -1|
Segue que:
x = Dx/D = 10/10 = 1,
y = Dy/D = 20/10 = 2
z = Dz/D = -30/10 = -3
OBSERVAÇÃO
Esta regra se aplica apenas para sistemas lineares nxn, em que o número de equações é igual ao número de incógnitas e o sistema for SPD.
EXERCÍCIO RESOLVIDO
04. Resolva usando a regra de Cramer:
{ x + y – z = 0
{ x – y – 2z = 1
{ x + 2y + z = 4
Abaixo uma figura que representa a resolução

Temos:
x = Dx/D = -15/-3 = 5
y = Dy/D = 6/-3 = -2
z = Dz/D = -9/-3 = 3
S {(5, 2,3)}
• Se (D ≠ 0), então o sistema será possível edeterminado (SPD);
• Se (D = 0), o sistema poderá ser possível eindeterminado ou impossível:
– Se Dx = Dy = Dz = ⋅⋅⋅ = 0, o sistema será possível e indeterminado (SPI).
– Se pelo menos um dos outros determinantes (Dx ;Dy ; Dz …) é diferente de zero, então o sistema e impossível (SI).



