Logaritmo – Propriedades e Exercícios

PROPRIEDADES DOS LOGARITMOS

Considere um número real n, e três números reais a, b e c, tais que 0 < a ≠ 1m, b > 0 e c > 0.
Dessa forma, temos:

LOGARITMO DO PRODUTO

Demonstração:

Considere três números reais w, j e k, tais que logᵃ (b.c) = w, logᵃb= j e logᵃ c=k.

Pela definição de logaritmo temos:

I. logᵃb = j ↔ aʲ = b
II. logᵃc = k ↔ aᵏ = c
III. logᵃ (b.c) = w ↔ aʷ = b.c

Substituindo (II) e (III) em (I), temos

aʷ = b . c = aʲ . aᵏ = a ʲ⁺ᵏ ⇒ aʷ = a ʲ⁺ᵏ ⇒ w = j+k

Logo, logᵃ (b.c) = logᵃ b+ logᵃc

Exemplo:

log⁵6= log⁵ 2.3 = log⁵2 + log⁵3

LOGARITMO DO QUOCIENTE

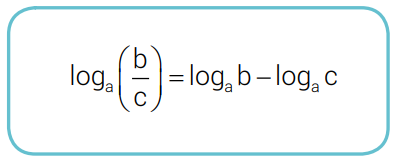
Demonstração:

A demonstração da 2ª propriedade é inteiramente análoga à feita na 1ª propriedade. Tente fazer!

Exemplo:

log⁵6 = log⁵ (12/2) = log⁵ 12 – log⁵2 

LOGARITMO DA POTÊNCIA

Demonstração:
Considere dois números reais w e j, tais que logᵃ bⁿ = w e logᵃ b = j.

Pela definição de logaritmo temos:

I. logᵃ bⁿ = w ↔ aʷ = bⁿ
II. logᵃ b = j ↔ aʲ = b

Elevando os membros da equação (II) a n, temos:

aʲ = b ⇒ (aʲ) = (b)ⁿ ⇒ aʲⁿ = bⁿ

Mas, na equação (I), temos que bⁿ = aʷ, substituindo temos:

aʲⁿ = aʷ ⇒ jn = w
Logo, logᵃ bⁿ = n.logᵃ b

Exemplo:
log² 3⁵ = 5.log² 3

OBSERVAÇÃO

• Se 0 < a ≠1, b > 0 e n ∈ ℕ*, então

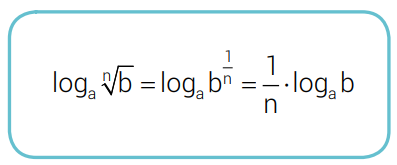
A demonstração dessa observação é análoga à feita na 3ª propriedade.
Tente fazer!

• Para relembrar, como já visto no módulo anterior, também temos que:

Se 0 < a ≠1, b > 0 e n ∈ ℝ*, então:

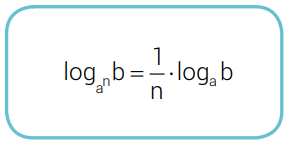
• Se b,c ∈ ℝ*, 0 < c ≠ 1, b > 0, então:

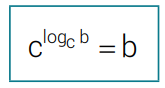
A demonstração dessa observação é análoga à feita na 3ª propriedade.

Tente fazer!

Exemplo:
5ˡᵒᵍ⁵ ⁷= 7

APLICAÇÕES DAS PROPRIEDADES

Sabendo que o log 2 = 0,3 e log 3 = 0,47, determine os logaritmos abaixo:

Exemplo1:

log6 = log2 3 log2 log3 0,3 0,47 0,77

Exemplo2:

log1,5 = log15/10 = log3/2 = log3 – log2 = 0,47 – 0,3 = 0,17

Exemplo3:

log² 1024 = log² 2¹⁰ = 10.log² 2 = 10.1 = 10

Exemplo 4:

log²⁵ 5 = log⁵ ²5 = 1/2 . log⁵5 = 1/2 . 1 = 1/2

Exemplo5:

3log³ ⁷= 3log³ ⁷= 7

Exemplo6:

log108=
Fatorando o 108, achamos que 108 = 2² . 3³
log108 = log2² . log3³ = log2² + log3³ = 2 . log2 + 3 . log3 =
2 . 0,3 + 3 . 0,47 = 2,01

Exemplo7:

8ˡᵒᵍ² ⁵ = 8ˡᵒᵍ² ⁵ = (2³) ˡᵒᵍ² ⁵ = 2³.ˡᵒᵍ² ⁵= ˡᵒᵍ² ⁵³ = 5³ = 125

EXERCÍCIOS RESOLVIDOS 

01. Se logx + logx² + logx³ + logx⁴ = –20 o valor de x é:

a) 10
b) 0,1
c) 100
d) 0,01
e) 1

Resolução: D

logx + 2.logx + 3.logx + 4.logx = -20
10logx = -20 →logx = -2
10-² = x → x = 0,01

02. Para quaisquer reais positivos A e B, o resultado da expressão log ᴀB³. log ʙA² é

a) 10
b) 6
c) 8
d) a.b
e) 12

Resolução: B

log ᴀB³. log ʙA² = 3.log ᴀB.2.log ʙA = 3 . 1/log ʙA . 2 . log ʙA = 3.2 = 6

OBSERVAÇÃO

O logaritmo decimal de 5 pode ser escrito de outra maneira:

log5 = log10/2 = log10 – log 2 = 1 = log2 

Assim, como o valor de log2 é um número irracional, é necessária uma aproximação e virá no enunciado para você.

OBSERVAÇÃO2

Apesar de utilizado em grande escala na Física, a terceira Lei de Kepler, assim como outras leis matemáticas, envolvem, sobretudo, proporcionalidades entre grandezas. No entanto, em alguns casos, transformá-las utilizando logaritmos pode ser útil para facilitar a extração de informações importantes. Portanto, deve-se estar atento à aplicação do logaritmo e suas propriedades em equações como a apresentada na questão a seguir.

EXERCÍCIO RESOLVIDO 

01. Um dos grandes legados de Kepler para ciência foi a sua terceira lei: “o quadrado do período de revolução de cada planeta é proporcional ao cubo do raio médio da respectiva órbita”. Isto é, sendo T o período de revolução do planeta e r a medida do raio médio de sua órbita, esta lei nos permite escrever que: T²= K · r³, onde a constante de proporcionalidade K é positiva.

Considerando x = log (T) e y = log (r), pode-se afirmar que:

Abaixo a figura que contém as alternativas da questão;

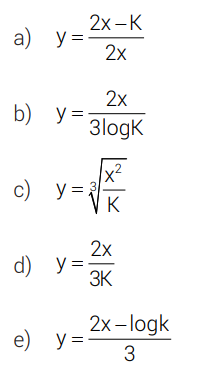
Resolução: E

No enunciado, foi dada a seguinte informação: T² = K.r³
Agora, aplicando em ambos os lados da igualdade teremos: logT² = log(K.r³)

Pela propriedade do produto teremos:
logT² = log k + log r³

Pela propriedade da potência:
2log T = log K + 3 log r

Substituindo os dados do enunciado:
2x = log k + 3 y

Portanto y = 2x – log k / 3