Geometria plana – Conceitos Básicos e Ângulos

O PONTO

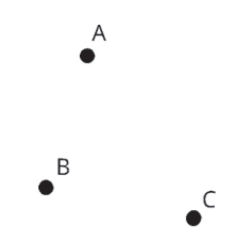
Os pontos costumam ser representados por letras maiúsculas do nosso alfabeto.

A RETA

As retas costumam ser representadas por letras minúsculas do nosso alfabeto. É importante lembrar que uma reta possui infinitos pontos.

Dados dois pontos distintos, existe uma única reta que passa por eles.

POSIÇÕES RELATIVAS ENTRE DUAS RETAS

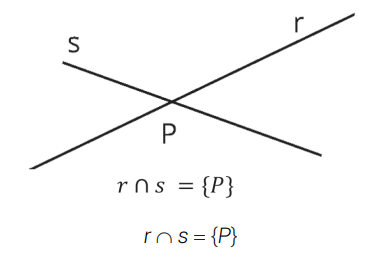
RETAS CONCORRENTES

Quando possuem um único ponto em comum.

RETAS PARALELAS

Quando não possuem ponto comum.

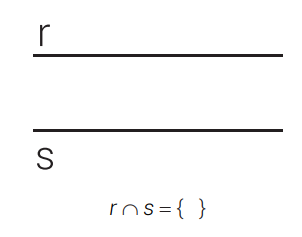
SUBCONJUNTOS DA RETA

SEMIRRETA

Nesse caso o ponto A é a origem da semirreta.

SEGMENTO DE RETA

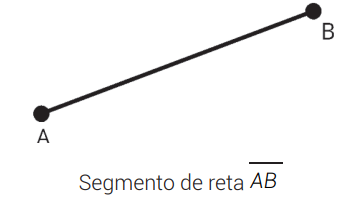
Segmento de reta com extremidades nos pontos A e B.

OBSERVAÇÃO

• Apesar da semirreta e do segmento de reta estarem contidos em uma reta, ambos possuem infinitos pontos.

• Pontos colineares são pontos que estão sobre uma mesma reta.

O PLANO

Os planos costumam ser representados por letras do alfabeto grego.

OBSERVAÇÃO

• Em um plano há infinitos pontos e retas.

• Três pontos não colineares, determinam um único plano que os contém.

• Pontos que estão sobre um mesmo plano são chamados de coplanares.

ÂNGULO

Chamamos de ângulo a parte do plano limitada por duas semirretas de mesma origem.

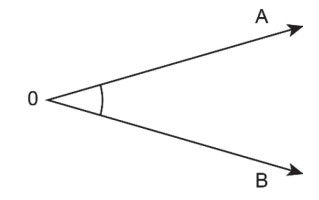
Ângulo AÔB, de vértice O e lados e .

A unidade de medida mais usada para o ângulo em geometria é o grau. Algumas medidas de ângulos recebem nomes especiais:

• Ângulo reto, quando mede 90°;

• Ângulo raso, quando mede 180° (meia-volta);

• Ângulo agudo, quando é menor do que 90°, mas não nulo;

• Ângulo obtuso, quando sua medida está entre 90° e 180°;  Dados dois ângulos α e β, dizemos que eles são:

• Complementares, quando α + β = 90°;

• Suplementares, quando α + β = 180°.

• Replementares, quando α + β = 360°. 

Dois ângulos são ditos congruentes quando têm as mesmas medidas. Assim, se dois ângulos AÔB e BÔC são ditos congruentes, podemos escrever que AÔB ≅ BÔC.

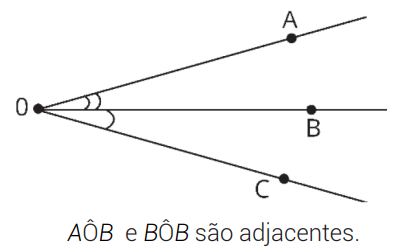
ÂNGULOS ADJACENTES

São ângulos que possuem um lado comum, mas não possuem região interna comum.

BISSETRIZ DE UM ÂNGULO

É a semirreta que divide o ângulo em dois ângulos congruentes.

ÂNGULOS OPOSTOS PELO VÉRTICE

São dois ângulos formados por duas retas concorrentes, como os ângulos α e β da figura. Ângulos opostos pelo vértice são sempre ângulos congruentes.

Exemplos:

01. Na figura,  e  são bissetrizes dos ângulos adjacentes  e respectivamente

Sabendo que e , calcule a medida do ângulo agudo .

Resolução:

Considere que AÔM =  x.

Dessa forma, como  é bissetriz de AÔB temos que MÔB = x.

Analogamente, considere que CÔN = y e como  é bissetriz de BÔC temos que NÔB = y.

Montamos agora um sistema pois sabemos que AÔN = 50° e NÔC = 30°.

Temos então que e finalmente que .

02. OX e OY ão bissetrizes dos ângulos adjacentes PÔQ e QÔR , respectivamente. Sabendo que o ângulos agudos PÔY e XÔR medem, respectivamente, 50º e 55º, calcule a medida do ângulo agudo PÔR.

Resolução:

É muito importante que nesses casos você consiga fazer um esboço da situação problema. Note que esse exemplo é análogo ao anterior (mudamos os valores e as letras!).

Considere que PÔX = a.

Dessa forma, como OX é bissetriz de PÔQ temos que XÔQ = a.

Analogamente, considere que RÔY = b e como OY é bissetriz de QÔR temos que YÔQ = b.

Montamos agora um sistema pois sabemos que
PÔY = 50º e XÔR = 55º.
PÔY = 50º = 2a + b
XÔR = 55º = a + 2b

Para resolver o sistema usaremos que b = 50 – 2a .
55 = a + 2(50 – 2a)
55 = a + 100 – 4a
55 – 100 = a – 4a
– 45 = – 3a
a = 15

Se a = 15 então b = 50 – 2·15 = 50 – 30 = 20 .

O ângulo PÔR é dado por 2a + 2b, portanto valerá 2·15 + 2·20 = 30 + 40 = 70.

ÂNGULOS FORMADOS POR RETAS PARALELAS CORTADAS POR UMA TRANSVERSAL

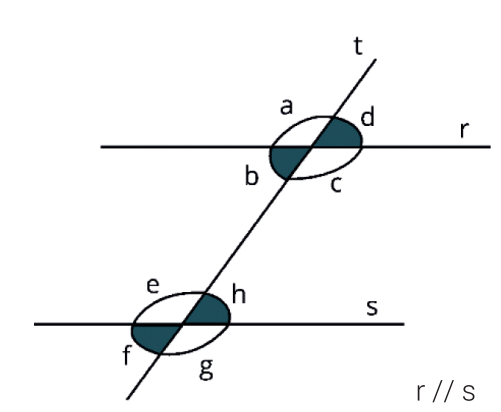
• Pares de ângulos

Correspondentes: a e e; b e f; d e h; c e g.
Alternos Internos: b e h; c e e.
Alternos externos: a e g; d e f.
Colaterais Internos: b e e; c e h.
Colaterais Externos: a e f; d e g.

Assim, é possível concluir que

• Um par de ângulos correspondentes são sempre congruentes, isto é, possuem a mesma medida.
• Um par de ângulos alternos são sempre congruentes.
• Um par de ângulos colaterais são sempre suplementares, isto é, somam 180º.

LEI ANGULAR DE TALES

Em qualquer triângulo, a soma dos ângulos internos mede 180º.

TEOREMA DO ÂNGULO EXTERNO

Em qualquer triângulo, a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele.

Exemplos:

01. Na figura, r // s // t:

Dessa forma, calcule as medidas dos ângulos indicados.

Solução:

É imediato que a = 130º (correspondente) e d = 60º (colateral interno do 120˚).

Sabendo que a vale 130º fica fácil perceber que b = 50º. Como b + c + d = 180º então calcularemos o valor de c.

Note que 50º + c + 60º = 180º → 110º + c = 180º → c = 70º

02. Na figura a seguir determine x sabendo que r // s e s // m.

Resolução:

Conhecendo o conceito de ângulos colaterais internos é fácil perceber que a = 150º e b = 140º. Dessa forma, podemos notar que a + b + x = 360º pois formam uma volta completa. Assim, 150º + 140º + x = 360º → 290º + x = 360º → x = 70º.