PRISMAS

Para definirmos um prisma, considere dois planos paralelos distintos, α e β e uma reta r secante a esses planos e um polígono convexo A¹A²A³….Aⁿ contido em α. Considere ainda todos os segmentos de reta paralelos a r, de modo que cada um deles tenha um extremo pertencente ao polígono e o outro extremo pertencente a β. A reunião de todos esses segmentos de reta é um poliedro chamado prisma convexo limitado ou, simplesmente, prisma.

As faces situadas nos planos paralelos α e β são chamadas de bases, a distância entre esses planos é chamada de altura do prisma, as arestas com extremidades nos dois planos são as arestas laterais e as faces na forma de paralelogramo, limitadas por duas arestas laterais consecutivas e duas arestas das bases são chamadas de faces laterais.

Na figura acima destacamos:

• Bases: A¹A²A³….Aⁿ e B¹B²B³….Bⁿ

• Arestas Laterais: A¹B¹, A²B², A³B³…., AⁿBⁿ.

• Faces Laterais: A1A²B²B¹,…. AⁿA¹B¹Bⁿ 

• Altura: h

CLASSIFICAÇÃO

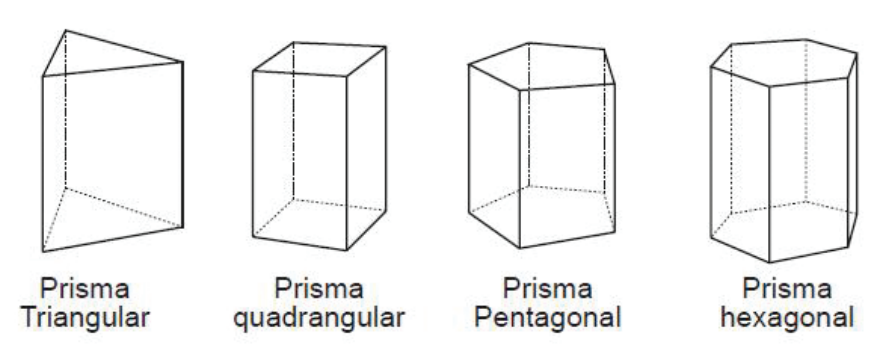
Um prisma é denominado de acordo com o número de lados das bases. Dessa maneira, um prisma cuja base é um triângulo é chamado de prisma triangular, um prisma cuja base é um quadrilátero é chamado prisma quadrangular, etc.

PRISMA RETO E PRISMA OBLÍQUO

Um prisma é chamado reto quando as arestas laterais são perpendiculares aos planos das bases. Os prismas que não são retos são chamados oblíquos.

PRISMA REGULAR

Chamamos de prisma regular todo prisma reto cujas bases são polígonos regulares.

Podemos ainda notar que toda face lateral de um prisma regular são retângulos congruentes.

PLANIFICAÇÃO DO PRISMA RETO

Observemos a seguir a planificação de um prisma triangular reto.

ÁREAS LATERAL E TOTAL

A soma das áreas de todas as faces laterais do prisma é denominada área lateral do prisma e a soma da área lateral com as áreas das duas bases é chamada de área total do prisma.

Aᵗᵒᵗᵃˡ = Aˡᵃᵗᵉʳᵃˡ + 2. Aᵇᵃˢᵉ

EXERCÍCIO RESOLVIDO

01. Cada uma das bases de um prisma reto com 10 cm de altura é um trapézio isósceles com lados 5 cm, 5 cm, 6 cm e
12 cm. Calcule a área lateral desse prisma.

Resolução:

A área lateral é a soma das áreas das faces laterais de um prisma, isto é, não usamos as áreas das bases. Nesse caso,
as bases são os trapézios, que devemos desconsiderar.

A área lateral dessa figura é composta por 4 retângulos, portanto a sua área lateral pode ser facilmente calculada.

Aᴸ = 5 . 10 + 6 . 10 + 5 . 10 + 12 . 10 = 50 + 60 + 50 + 120 = 280 cm².

VOLUMES

Intuitivamente, o volume de um sólido é a quantidade de espaço por ele ocupado. Para exprimir essa quantidade de espaço através de um número, devemos compará-la com uma unidade. Chamamos de volume o resultado dessa comparação.

UNIDADES DE VOLUME

Considere um cubo com 1 cm de aresta. A porção do espaço ocupada por esse cubo é uma unidade de volume definida como 1 cm³ (lemos: “um centímetro cúbico”).

Para cada unidade de comprimento, temos uma unidade correspondente de volume.

Definimos então de maneira análoga 1 mm³, 1 dm³, 1 m³, 1 dam³, 1 hm³ e 1 km³ como a porção do espaço ocupada por cubos com arestas de 1 mm, 1 dm, 1 m, 1 dam, 1 hm e 1 km, respectivamente.

Essas unidades podem ser representadas na escala a seguir.

Note que cada unidade dessa escala vale 1.000 vezes a unidade imediatamente à sua direita.

Para ilustrar a situação, observe o cubo abaixo de lado 1 metro, dividido em 1000 cubinhos de aresta 1 dm, que por sua vez pode ser dividido em 1000 outros cubinhos de aresta 1 cm.

Outra unidade usada para medir volumes é o litro (L), que é definido como 1 dm³.

1 L = 1 dm³

As unidades derivadas do litro podem ser expressas na escala abaixo, onde cada unidade vale dez vezes a unidade imediatamente à sua direita.

Observe que 1 mL = 1 cm³.

PARALELEPÍPEDO RETÂNGULO

O paralelepípedo retângulo, ou simplesmente um bloco retangular, é um poliedro formado por 6 retângulos. Ele fica perfeitamente determinado por três medidas: o seu comprimento (a), a sua largura (b) e a sua altura (c).

VOLUME DO PARALELEPÍPEDO RETÂNGULO

Observe que em um paralelepípedo retângulo de comprimento a, largura b e altura c, pode ser dividido em a . b . c cubos unitários.

Assim, o volume do paralelepípedo retângulo é:

Vᵖᵃʳᵃˡᵉˡᵉᵖⁱᵖᵉᵈᵒ = a . b . c 

OBSERVAÇÃO

Podemos dizer ainda que o volume de um paralelepípedo retângulo é calculado pelo produto da área da base pela altura:

Vᵖᵃʳᵃˡᵉˡᵉᵖⁱᵖᵉᵈᵒ = aᵇᵃˢᵉ . hᵃˡᵗᵘʳᵃ

ÁREA TOTAL DO PARALELEPÍPEDO RETÂNGULO

Observe que das 6 faces retangulares de um paralelepípedo retângulo de dimensões a, b e c, temos 2 retângulos com base a e altura b, 2 com base a e altura c e 2 com base b e altura c. Logo a soma das áreas desses retângulos são:

Aᵗᵒᵗᵃˡ = 2 . ab + 2 . ac + 2 . bc 

Aᵗᵒᵗᵃˡ = 2(ab + ac + bc) 

DIAGONAL

Para calcular a diagonal do paralelepípedo retângulo acima ABCDEFGH, observemos o triângulo retângulo BDH destacado acima. Note que a hipotenusa BH é a diagonal do paralelepípedo. Observe ainda que no triângulo ABD, temos que d² = a² + b², assim no triângulo BDH temos D² = d² + c2 e portanto, D² = a² + b² + c².

EXERCÍCIO RESOLVIDO

02. Dado um paralelepípedo retângulo de arestas iguais a 3 cm, 4 cm e 12 cm, determine a sua área total, a diagonal e o volume.

Resolução:

a = 3, b = 4 e c = 12.

Aᵗᵒᵗᵃˡ = 2(ab + ac + bc)

Aᵗᵒᵗᵃˡ = 2( 3 . 4 + 3 . 12 + 4 . 12) = 2(12 + 36 + 48) = 2(96) = 192cm² 

D² = a² + b² + c²

D² = 3² + 4² + 12² 

D² = 9 + 16 + 144 = 169 

D = 13cm 

Vᵖᵃʳᵃˡᵉˡᵉᵖⁱᵖᵉᵈᵒ = a . b . c 

Vᵖᵃʳᵃˡᵉˡᵉᵖⁱᵖᵉᵈᵒ = 3 . 4 . 12 = 144cm³ 

CUBO

O cubo é um bloco retangular de arestas com a mesma medida, ou seja, um paralelepípedo retângulo, onde todas as arestas medem a.

VOLUME DO CUBO

Calculamos o volume de modo análogo ao paralelepípedo retângulo. Assim, o volume do cubo de aresta a será V = a . a . a.

Vᶜᵘᵇᵒ = a³ 

ÁREA TOTAL

Observemos que o cubo de aresta a contém 6 quadrados de lado a. Logo:

Aᵗᵒᵗᵃˡ = 6 . a² 

DIAGONAL

Considere a seguir o cubo ABCDEFGH, de aresta a.

Note que a diagonal do cubo BH forma um triângulo retângulo com a aresta a e a diagonal da face BD. Logo, D² = d²+ a², mas no triângulo ABD, temos que d²= a² + a² = 2a². Portanto, D² = a² + 2a² = 3a² e assim:

Dᶜᵘᵇᵒ = a√3

EXERCÍCIO RESOLVIDO 

03. A medida do volume de um cubo, em cm³ , é igual à medida de sua área total, em cm² . Determine a medida da diagonal desse cubo.

Resolução:

Vᶜᵘᵇᵒ = a³ e Aᵗᵒᵗᵃˡ = 6 . a², igualando as duas fórmulas encontramos o valor da aresta. 

Note que a³ = 6a² implica em a = 6

Dessa podemos calcular a diagonal, pois Dᶜᵘᵇᵒ = a√3

Dᶜᵘᵇᵒ = 6√3cm

PRINCÍPIO DE CAVALIERI

Para entender esse princípio, façamos a seguinte experiência:

Coloque em cima da mesa uma resma de papel. Ela perfeitamente arrumada é um paralelepípedo retângulo e, dessa maneira, já sabemos calcular seu volume. Podemos transformar o paralelepípedo retângulo em um outro paralelepípedo, só que oblíquo, encostando uma régua nas faces laterais, ou ainda, usando as mãos, poderemos moldar um sólido diferente como a figura abaixo exemplifica.

Observe que os sólidos possuem volumes iguais. De modo mais geral, suponha que dois sólidos A e B estão apoiados num plano horizontal e que qualquer outro plano também horizontal corte ambos segundo seções de mesma área. O Princípio de Cavalieri afirma que o volume de A é igual ao volume de B.

VOLUME DO PRISMA

Suponha agora que um prisma e um paralelepípedo retângulo com a mesma altura, mesma área da base Aᴮ e apoiados sobre um mesmo plano horizontal, sejam cortados por um outro plano horizontal, e produzem seções de áreas A¹ e A² no paralelepípedo e no prisma, respectivamente.

Como A¹= Aᴮ = A² , pelo princípio de Cavalieri, o volume de um
prisma pode ser sempre calculado pelo produto da sua área da base pela altura.

Vᵖʳⁱˢᵐᵃ  = Aᵇᵃˢᵉ . h