Princípios da óptica, reflexão e espelhos planos

A LUZ

Definimos como luz uma energia radiante que através dos nossos órgãos visuais nos causa a sensação da visão. Diz-se que a luz é uma energia radiante, pois ela se propaga por meio de ondas eletromagnéticas.

Uma característica importantíssima das ondas eletromagnéticas é a sua enorme velocidade. Todas as ondas eletromagnéticas possuem a mesma velocidade no vácuo que é representada pela letra C e corresponde a maior velocidade possível na natureza. A velocidade da luz no vácuo vale, aproximadamente:

c = 300.000 km/s = 3 . 10⁵ km/s = 3 . 10⁸ m/s

Como já foi dito, a velocidade da luz possui este valor no vácuo. Nos meios materiais, a velocidade será menor e diferente para cada onda eletromagnética.

Ano-luz é uma unidade de distância e corresponde à distância percorrida pela luz no vácuo em um ano.

1 ano-luz = 9,5 x 10¹² km

FONTES DE LUZ

Uma fonte de luz é qualquer corpo visível, isto é, que emite luz para os nossos olhos.

As fontes podem ser classificadas em:

• Corpo luminoso ou fonte primária: são os que possuem luz própria: O Sol, uma lâmpada ou uma vela acesa etc.

• Corpo iluminado ou fonte secundária: são os que não possuem luz própria, eles apenas refletem a luz que incide sobre eles: a Lua, esta apostila que você está lendo, você etc.

• Fonte pontual ou puntiforme: são aquelas que possuem dimensões desprezíveis em face de outras dimensões envolvidas: uma estrela nos parecerá um pontinho luminoso, uma lâmpada bem distante do observador também será uma fonte pontual.

• Fonte extensa: uma fonte é dita extensa quando não é possível desprezar suas dimensões: uma lâmpada fluorescente próxima do observador.

RAIOS DE LUZ E FEIXES DE LUZ

Raio de Luz: é a representação da trajetória da luz, que indica sua direção e sentido. De cada ponto de uma fonte de luz saem infinitos raios de luz.

Feixe Cônico Convergente: todos os raios de luz convergem para um mesmo ponto. Consegue-se um feixe convergente com a ajuda de uma lente convergente, por exemplo.

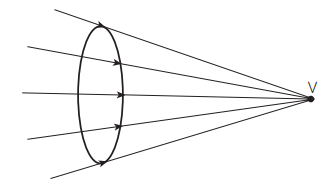
Feixe Cônico Divergente: todos os raios de luz divergem de um mesmo ponto. Num farol de automóvel o feixe é divergente, emitida numa direção tal que não atrapalhe a visão do motorista que vem em sentido contrário.

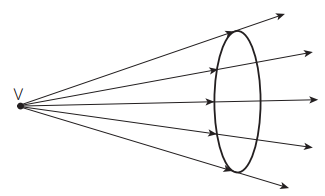
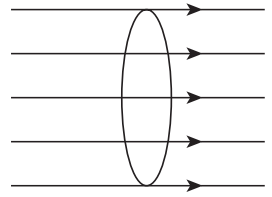
Feixe Cilíndrico Paralelo: os raios luminosos são paralelos. Nos holofotes, o feixe de luz é cilíndrico paralelo

MEIO DE PROPAGAÇÃO

Quanto à propagação da luz, os meios podem ser classificados em:

• transparente – é aquele meio que permite a visualização nítida dos objetos, pois a luz se propaga em trajetórias bem definidas;

• translúcido – permite a visualização não claramente, devido às trajetórias distorcidas da luz;

• opaco – não ocorre propagação da luz.

PRINCÍPIOS DA ÓPTICA GEOMÉTRICA

Os princípios que serão estudados são necessários no estudo das trajetórias descritas pela luz na sua propagação. Estudaremos os três princípios mais importantes.

PRINCÍPIO DA INDEPENDÊNCIA DOS RAIOS LUMINOSOS

Afirma que os raios de luz são independentes, isto  é, mesmo ocorrendo o cruzamento, um raio não afeta a trajetória do outro.

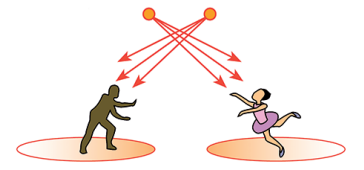
A figura anterior, em que duas áreas são iluminadas por holofotes, exemplifica bem a independência dos raios luminosos.

PRINCÍPIO DA PROPAGAÇÃO RETILÍNEA DA LUZ

Nos meios transparentes, homogêneos e isótropos, a luz se propaga em linha reta. Um grande exemplo para este princípio acontece quando raios de luz solar penetram através de uma janela de uma sala.

PRINCÍPIO DA REVERSIBILIDADE DOS RAIOS LUMINOSOS

Por um princípio conhecido como da mínima-ação, sabemos que a luz percorre entre dois pontos o caminho de menor “esforço”. Portanto, se a luz descreve uma trajetória do ponto A ao ponto B, o caminho contrário, ou seja, do ponto B ao ponto A, será exatamente o mesmo.

APLICAÇÕES DOS PRINCÍPIOS DA ÓPTICA

A seguir, veremos alguns fenômenos físicos que podem ser explicados através dos princípios da óptica geométrica:

SOMBRA

Na figura abaixo podemos identificar uma fonte luminosa puntiforme representada por F, um disco opaco D e um anteparo A.

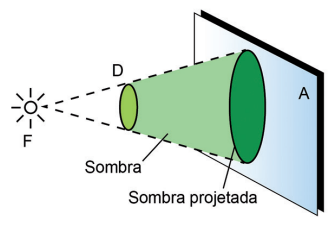
Entre o disco e o anteparo, observa-se uma área que não é iluminada pela fonte F e, considerando esta como a única fonte luminosa, esta região não iluminada consistirá em uma sombra. No anteparo, como está na figura, ocorre uma região denominada de sombra projetada.

SOMBRA E PENUMBRA

Se um sistema for iluminado por uma fonte extensa ao invés de uma fonte pontual, ocorrerá, além das regiões de sombra e sombra projetada, áreas de penumbra e penumbra projetada, que consistem em regiões que são parcialmente iluminadas e serão uma transição entre áreas perfeitamente iluminadas a áreas de sombra total.

ECLIPSES

Os casos mais importantes de sombra e penumbra são os eclipses solares e lunares.

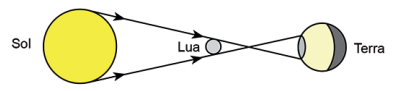
O eclipse lunar acontece quando a Lua penetra no cone de sombra da Terra, como mostra a figura abaixo. Os eclipses lunares ocorrem somente em Lua cheia.

Cone de sombra da terra

Os eclipses solares são mais amplos. Existem os eclipses anulares, que ocorrem quando o cone de sombra da lua se fecha antes da Terra e permanece apenas a penumbra projetada. A figura abaixo exemplifica um eclipse anular.

O eclipse do Sol ocorre na Lua nova e, neste caso, a Lua projeta sobre a Terra uma região de sombra projetada, eclipse total, e uma região de penumbra projetada.

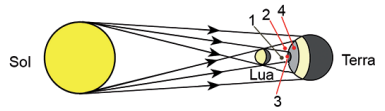
• Região 1 = cone de sombra da Lua

• Região 2 = penumbra

• Região 3 = sombra da Lua projetada na Terra. Nessa região ocorre o eclipse total do Sol.

• Região 4 = penumbra projetada. Nessa região ocorre o eclipse parcial do Sol, caso em que uma parte do “disco solar” permanece visível.

FASES DA LUA

A Lua gira em torno da Terra em uma órbita elíptica levando aproximadamente 27,3 dias para completar uma volta. Durante este período, dependendo de sua posição, a Lua é vista de formas diferentes da Terra. Essas formas diferentes como a Lua é iluminada denominam-se de fases da Lua.

Na Lua Nova, o hemisfério voltado para a Terra não é iluminado, e na Lua Cheia, o hemisfério em questão é totalmente iluminado. Nas fases denominadas de Quarto- Crescente e Quarto-Minguante, o hemisfério voltado para a Terra é parcialmente iluminado. Na figura abaixo, estão todas as fases da Lua.

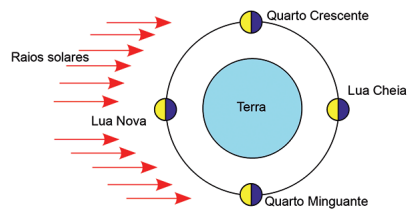
Apenas uma das faces da Lua permanece voltada para a Terra, isso acontece pois o período de rotação em torno do seu próprio eixo é igual ao seu período de translação em torno da Terra. O lado oculto ou lado negro da Lua já foi tema de muitas abordagens na Arte, como o cinema e a música.

OBSERVAÇÃO

COMO ECLIPSE PODE CAIR NO ENEM?

O eclipse solar é um fenômeno que ocorre de tempos em tempos, porém, só é possível observá-lo em determinadas posições do planeta, devido às dimensões do Sol e da Lua. A questão aborda a relação entre a sombra vista em um eclipse solar e a posição em que se encontra o observador.

EXERCÍCIO RESOLVIDO

01. (ENEM) A figura abaixo mostra um eclipse solar no instante em que é fotografado em cinco diferentes pontos do planeta.

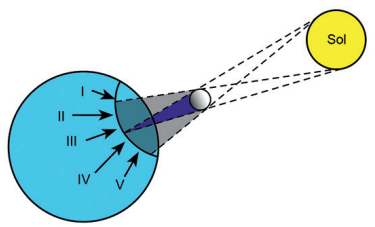
Três dessas fotografias estão reproduzidas abaixo.

As fotos poderiam corresponder, respectivamente, aos pontos:
a) III, V e II
b) II, III e V
c) II, IV e III
d) I, II e III
e) I, II e V
Resolução: A

CÂMARA ESCURA

Na figura a seguir podemos identificar uma câmara escura com um orifício e diante desta caixa, no lado que contém o orifício, há um objeto luminoso AB. Os raios que partem do objeto AB atravessam o orifício O, penetram na câmara e projetam na parede oposta uma imagem semelhante ao objeto, porém invertida.

Pela geometria concluímos que os triângulos OAB e OA’B’ são semelhantes, desta forma:

Sendo AB e A’B’ os comprimentos do objeto e da imagem e a e b as distâncias entre o objeto e o orifício e a imagem e o orifício, respectivamente.

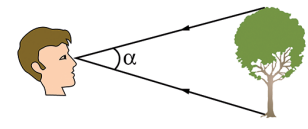
ÂNGULO VISUAL

O ângulo visual representado na figura a seguir por α, corresponde ao ângulo formado pelos raios que ligam as extremidades do objeto e os olhos do observador.

REFLEXÃO DA LUZ E ESPELHOS PLANOS

A reflexão da luz ocorre quando um raio luminoso atinge uma superfície e retorna para o meio no qual se propagava.

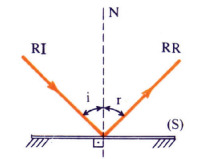
Os elementos que devem ser conhecidos:

RI → Raio Incidente.

RR → Raio Refletido.

N → Normal no ponto de incidência.

(S) → Símbolo de superfície plana refletora: o espelho plano.

As reflexões podem ser classificadas em:

• Reflexão Regular ou Especular: Raios incidentes paralelos refletem paralelos. É a que ocorre numa superfície polida. É a que estudaremos no nosso curso.

• Reflexão Difusa: Raios incidentes paralelos não refletem paralelos.

A reflexão regular ou especular é regida pelas seguintes leis:

1ª LEI: O raio incidente, a normal no ponto de incidência e o raio refletido estão no mesmo plano (são coplanares).

2ª LEI: O ângulo de incidência (i) é igual ao ângulo de reflexão (r).

EXERCÍCIO RESOLVIDO

02. (UECE) Dois espelhos planos são dispostos paralelos um ao outro e com as faces reflexivas viradas uma para outra. Em um dos espelhos incide um raio de luz com ângulo de incidência de 45º. Considerando que haja reflexão posterior no outro espelho, o ângulo de reflexão no segundo espelho é

a) 45º.
b) 180º.
c) 90º.
d) 22,5º.
e) 10,0°.

Resolução: A
Construindo os raios incidentes e refletidos:

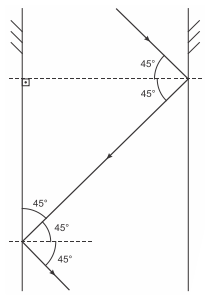
De acordo com a figura, podemos concluir que o ângulo de reflexão no segundo espelho é de 45º.

REFLEXÃO SELETIVA DA COR DOS CORPOS

A luz branca (policromática) é a mistura de todas as cores (monocromáticas) básicas do “arco-íris”: vermelho, alaranjado, amarelo, verde, azul, anil e violeta. Lembrando que existem vários tons, portanto as sete cores do arco-íris na verdade são diversas cores formando um espectro contínuo.

Um corpo que apresenta aos nossos olhos a cor vermelha é porque ele tem a capacidade de refletir apenas a luz vermelha, qualquer cor que incida sobre ele será absorvida, assim é também com outras cores: um corpo é azul se tem a capacidade de refletir o azul e absorver as outras cores. Um corpo verde se apresentará com a cor verde se for iluminado pela luz branca (já que ela contém a verde) ou por uma mistura qualquer que contenha verde, caso contrário ele se apresentará aos nossos olhos como negro.

OBSERVAÇÃO

Existe também o fenômeno da refração seletiva e acontece quando uma luz policromática incide em uma superfície monocromática que funciona como um filtro. Neste caso, se a luz policromática possuir a cor do filtro, este permitirá que somente esta luz passe. Na figura abaixo, a luz branca incide em um filtro vermelho e somente a luz vermelha emergirá do filtro.

ESPELHOS PLANOS

O espelho plano é o sistema óptico mais simples de ser estudado e é também o mais facilmente encontrado no dia a dia. Constitui-se de uma superfície polida onde ocorre predominantemente a reflexão da luz. No estudo de suas propriedades utilizaremos, basicamente, os princípios da óptica geométrica.

IMAGEM CONJUGADA POR UM ESPELHO PLANO

Para estudarmos o comportamento da imagem de um ponto material produzida por um espelho plano, consideraremos um ponto P diante um espelho. A luz que parte de P incide obliquamente no espelho e sofre reflexão. A figura ao lado ilustra a situação e podemos perceber que os prolongamentos dos raios refletidos irão se cruzar no ponto P’, por onde também passa a reta normal (reta perpendicular ao sistema óptico). O observador enxerga o ponto P’ como imagem do ponto P.

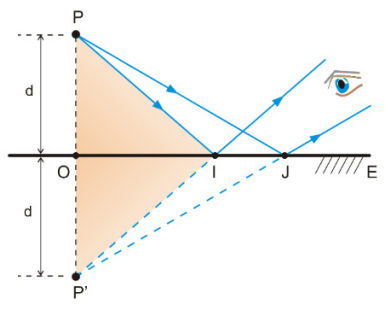
Sobre a imagem é importante saber que ela e o objeto são simétricos em relação ao espelho plano, ou seja, a distância do objeto ao espelho é igual a deste à imagem e pertencem a mesma reta normal à superfície do espelho. Esta propriedade dos espelhos planos, da imagem ser simétrica ao objeto, é conhecida como Propriedade Fundamental dos Espelhos Planos.

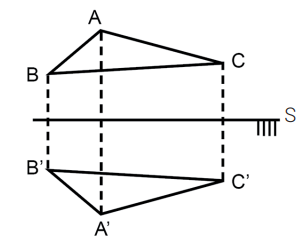
O estudo torna-se um pouco mais complexo se tratarmos de corpos extensos, porém a propriedade da simetria continuará a ser aplicada. Quando tratamos de corpos extensos dizemos que o objeto e a imagem são enantiomorfos e isso significa, que o lado direito do objeto corresponde ao esquerdo da imagem. Na figura acima um triângulo ABC foi colocado diante de um espelho plano formando uma imagem dele enantiomorfa. Observe que as distâncias de A, B e C ao espelho são iguais, respectivamente, as distâncias do espelho as suas imagens A’, B’ e C’.

Pegaremos como exemplo agora a palavra FÍSICA. Se colocarmos um espelho à sua direita, teremos a seguinte imagem:

O aluno fatalmente encontrará questões que se referem a palavras, figuras ou objetos, como relógios diante de espelhos e perguntas a respeito da imagem conjugada. Algumas figuras que possuem um eixo de simetria, como a letra A, por exemplo, não apresentarão problemas, mas na maioria deve-se identificar a imagem enantiomorfa.

Uma maneira prática de obtermos a imagem corretamente seria escrevermos a palavra ou figura em uma folha de papel, girarmos a folha ao redor da borda onde estaria o espelho e olharmos as costas da folha.

A “sombra” da palavra vista por trás corresponde à imagem do objeto obtida pelo espelho.

EXERCÍCIO RESOLVIDO

03. (UERN) Na noite do réveillon de 2013, Lucas estava usando uma camisa com o ano estampado na mesma. Ao visualizá-la através da imagem refletida em um espelho plano, o número do ano em questão observado por Lucas se apresentava da seguinte forma

Resolução: B
No espelho plano, objeto e imagem são simétricos em relação ao plano do espelho. Como consequência, a imagem
é enantiomorfa em relação ao objeto.

CAMPO VISUAL

O campo visual corresponde à área que pode ser visualizada pelo observador olhando para o espelho.

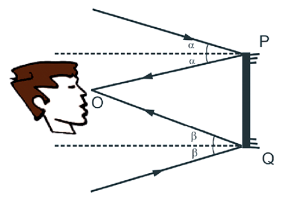
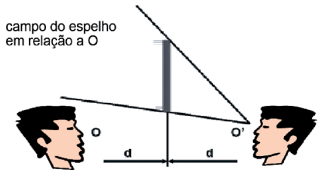
O campo visual pode ser facilmente determinado traçando-se raios ligando o observador aos extremos do espelho que sofrerão reflexão. A área compreendida entre os raios refletidos determinará o campo visual. Para traçarmos os raios refletidos devemos obter a posição simétrica do observador e traçar retas que liguem esta posição aos extremos dos espelhos, como mostra a figura abaixo:

TRANSLAÇÃO DE UM ESPELHO PLANO

O movimento de translação de um espelho plano consiste em deslocar o espelho no mesmo eixo onde se encontra o objeto. Na figura abaixo temos um espelho plano que foi deslocado horizontalmente para direita de uma distância x. Com isso a imagem se deslocou de y. Pela figura deduz-se que

OBSERVAÇÃO

Observe o esquema que mostra um espelho E que se desloca uma distância x, produzindo um deslocamento y na imagem de um objeto que permanece em repouso em relação ao solo.

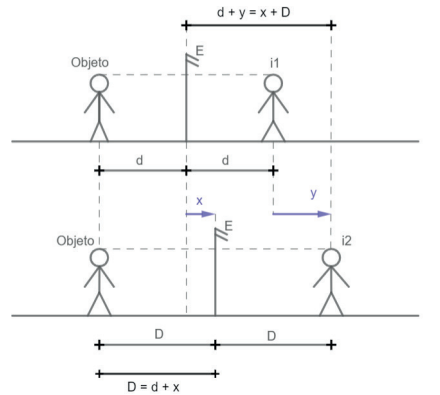
Conseguimos pela imagem, lembrando da propriedade de simetria, duas relações:

D = d + x (eq.1)
d + y = D + x (eq.2)

Somando as equações 1 e 2, temos:

D + d + y = d + x + D + x
y = 2·x

Observa-se que a distância y percorrida pela imagem é o dobro da distância x percorrida pelo espelho. Resumindo, se o espelho se afastar 1 metro do objeto, a imagem vai se afastar 2 metros do objeto; caso o espelho se afaste 4 metros do objeto, a imagem vai se afastar 8 metros do objeto.

OBSERVAÇÃO

Caso o objeto se movimente em relação ao espelho com velocidade v de aproximação, a imagem também se aproximará com velocidade v, em módulo.

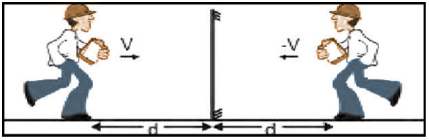
Caso o objeto se afaste, a imagem também se afastará do espelho, porém, o módulo da velocidade será sempre o mesmo. Se o objeto permanece parado em relação ao solo e o espelho se desloca com velocidade de módulo igual a v, a imagem se deslocará com velocidade igual a 2v em relação ao objeto e V em relação ao próprio espelho.

EXERCÍCIO RESOLVIDO

04. (UEMG) Um espelho reflete raios de luz que nele incidem. Se usássemos os espelhos para refletir, quantas reflexões interessantes poderíamos fazer. Enquanto a filosofia se incumbe de reflexões internas, que incidem e voltam para dentro da pessoa, um espelho trata de reflexões externas.

Mas, como escreveu Luiz Vilela, “você verá.”

Você está diante de um espelho plano, vendo-se totalmente. Num certo instante, e é disso que é feita a vida, de instantes, você se aproxima do espelho a 1,5 m/s e está a 2,0 m de distância do espelho.

Nesse instante, a sua imagem, fornecida pelo espelho, estará

a) a 2,0 m de distância do espelho, com uma velocidade de 3,0 m / s em relação a você.

b) a 2,0 m de distância do espelho, com uma velocidade de 1,5 m / s em relação a você.

c) a uma distância maior que 2,0 m do espelho, com uma velocidade de 3,0 m / s em relação ao espelho.

d) a uma distância menor que 2,0 m do espelho, com uma velocidade de 1,5 m / s em relação ao espelho.

e) a 4,0 m de distância do espelho, com uma velocidade de 1,5 m/s em relação a você.

Resolução: A

Num espelho plano, objeto e respectiva imagem são simétricos em relação ao plano do espelho. Portanto, quando você está a 2 m do espelho sua imagem também está a 2 m dele. Devido a essa mesma propriedade (simetria) a velocidade da imagem em relação ao espelho é, em módulo, igual à do objeto, porém em sentido oposto.

Assim, se você se aproxima do espelho com velocidade de módulo 1,5 m/s sua imagem também se aproxima com 1,5 m/s. Então, relativamente a você, a velocidade de sua imagem tem módulo 3,0 m/s.

Rotação do espelho plano

O movimento de rotação do espelho plano acontece quando um espelho plano gira ao redor de um ponto fixo (ponto C da figura). Sobre este movimento podem ser feitas duas perguntas: o desvio angular do raio incidente e a velocidade angular da imagem.

Quando giramos um espelho de um ângulo igual a θ o raio refletido também sofre um desvio. Representaremos esse desvio por Δ.

Na figura, os ângulos internos do triângulo CAB são, θ, 90°+ α e β, logo:

θ + 90º + α + β = 180° ⇒ θ = 90° – α – β

No triângulo ABD temos:

Δ + 2α + 2β = 180° ⇒ Δ = 180° – 2α – 2β ⇒ Δ = 2 (90° – α – β)
Logo: Δ = 2q

Além do raio refletido, a imagem também se altera. A figura ao lado P’ é a primeira imagem formada e P’’ é a imagem formada após o deslocamento angular do espelho. A imagem executa um movimento circular. O ângulo q corresponde ao deslocamento angular da imagem e vale o dobro do deslocamento do espelho.

Dessa forma, se imaginarmos a velocidade angular do espelho (wE) e da imagem (wi), teremos a seguinte relação:

wi = 2wE

EXERCÍCIO RESOLVIDO 

05. (UNESP) Um raio de luz, vertical, incide num espelho plano horizontal. Se o espelho girar 20 graus em torno de
um eixo horizontal, o raio refletido se desviará de sua direção original de

a) 0°
b) 20°
c) 10°
d) 60°
e) 40°

Resolução: E
∆ = 2 . θ
∆ = 2 . 20º
∆ = 40º

Associação de espelhos planos

Podemos obter inúmeras imagens através da associação de espelhos planos. Isso se deve a propriedade dos espelhos planos de sua imagem também se constituir em um espelho. Na figura abaixo, temos um ponto P entre dois espelhos planos que formam um ângulo α.

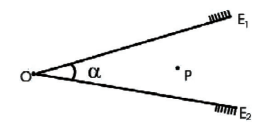
O número de imagens formadas pode ser obtido através da fórmula:

n = 360° – 1
            α

Porém, deve-se ter atenção, pois caso n seja ímpar, a fórmula é aplicada para qualquer posição de P. Se n for par, seu valor será correto somente se P estiver a uma mesma distância dos espelhos.

Pela figura a seguir verificamos que a conjugação de imagens só não ocorre quando a imagem se encontra na chamada zona morta.

Os pontos P’’2 e P’’1 constituem somente uma imagem.

É válido lembrar que as imagens formadas por reflexão simples (somente uma reflexão) serão enantiomorfas, porém as imagens formadas por duas reflexões serão iguais ao objeto. Assim sendo, as imagens formadas por número ímpar de reflexões serão enantiomorfas e as formadas por número par serão iguais ao objeto.

EXERCÍCIO RESOLVIDO 

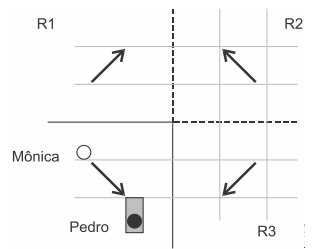
06. (FCMMG) Dois espelhos perpendiculares entre si estão posicionados em paredes verticais de um shopping. Mônica move-se entre eles na direção de Pedro, que está sentado num banco, também entre os espelhos, como mostrado na figura, vista do alto.

Pedro observa três imagens da Mônica, através dos espelhos, nas regiões R1, R2 e R3. O sentido do movimento de Mônica observado por Pedro na região R2 é representado pela seta:

Resolução: C
Fazendo o desenho do movimento da Mônica e rebatendo-o nos espelhos, temos:

Dimensão do espelho plano

Vamos obter o tamanho mínimo do espelho para que uma pessoa possa se ver por inteiro.

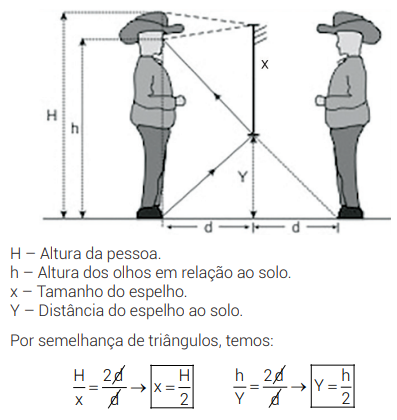
O espelho precisa ter, no mínimo, metade da altura da pessoa, além de estar localizado a uma distância do solo que igual à metade da altura dos olhos da pessoa em relação ao chão.

Exercício Resolvido

07. (UFJF-PISM 2) Manuela deve comprar um espelho para instalar em seu quarto. Ela pretende comprar um espelho que permita ver sua imagem completa refletida nele. Sabendo que Manuela tem 1,70 m de altura e que seus olhos estão a 1,55 m do chão, ajude-a a realizar sua escolha, calculando o que se pede.

a) A máxima altura em relação ao solo onde pode ser colocada a base do espelho.

b) A altura mínima em relação ao solo onde pode ser colocado o topo do espelho.

Resolução:
Dados: H = 1,70 m; h = 1,55 m.

Considerando que o referido espelho seja plano, objeto e imagem são simétricos em relação ao plano do espelho. A
figura ilustra a situação.

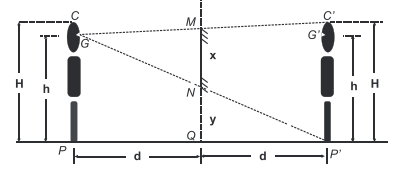
a) Seja y a distância da borda inferior do espelho ao solo e d a distância de Manuela ao espelho.
Por semelhança de triângulos:

ΔNQP’ ≈ ΔGPP’ ⇒ y/d = h/2d ⇒ y = h/2 = 1,55/2 ⇒ y = 0,775 m.

b) Por semelhança de triângulos, encontra-se também a altura mínima x desse espelho:

ΔGMN ≈ ΔGC’P’ ⇒ x/d = H/2d ⇒ x = H/2 = 1,70/2 ⇒ x = 0,85 m.

A distância do topo do espelho ao solo é:
Hᵉ = x + y = 0,85 + 0,775 ⇒ Hᵉ = 1,625 m.