Podemos imaginar também um carro em movimento. É a força gerada pelo motor que faz a velocidade do carro aumentar, aumentando, consequentemente, a sua energia. Quando os freios são acionados, o atrito entre o pneu e o asfalto faz a velocidade diminuir, ou seja, a energia do carro começa a diminuir.

Quando um agente externo realiza uma força sobre um sistema fazendo com que a velocidade do sistema sofra variações, dizemos que esse agente externo está realizando um trabalho (W) sobre o sistema.

Essa variação de velocidade pode ser traduzida como variação de energia (cinética) do sistema. A energia total de um corpo chama-se energia mecânica (E), que é a soma de duas outras energias: energia potencial () e energia cinética ():

e

Ou seja, energia cinética é a que muda quando há um trabalho sendo realizado pelo sistema (W > 0) ou sobre o sistema (W < 0).  Supondo que haja n forças atuando em um corpo, se a velocidade aumentar, o trabalho resultante (W_r) é positivo, se diminuir, é negativo. Essa equivalência entre trabalho e energia cinética é chamada de teorema trabalho – energia.

ENERGIA CINÉTICA DE UM CORPO DE MASSA M:

Então:

Lembrando-se de produto escalar, temos que:

E que todo produto escalar gera um escalar. Ou seja, trabalho é uma grandeza escalar.

Onde θ é o ângulo entre os vetores força () e deslocamento ().

A unidade de energia do S.I. é J (Joule).

Exemplo 1

Uma bolinha de 2 kg é abandonada a uma altura de 5 m. Desprezando a resistência do ar, responda as perguntas abaixo:

A) Qual a variação de energia cinética da bolinha do instante inicial até o momento em que toca no solo?

B) Qual a velocidade final da bolinha?

Resolução:

A) A variação de energia cinética corresponde ao trabalho da força resultante. Como a única força que atua no corpo é a força peso, podemos dizer que:

Note que o ângulo entre os vetores peso  e deslocamento  vale zero.

B) 

Exemplo 2

Um bloco de pedra, de 40 kg, desce um plano inclinado a partir do repouso, deslizando sobre rolos de madeira, sem atrito.

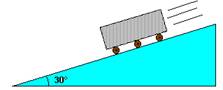
Sabendo-se que o plano inclinado mede 12 m, calcule o trabalho resultante das forças que atuam no bloco.

Resolução:

As forças que atuam no bloco são peso e normal. Como a normal é perpendicular ao vetor deslocamento, ela não irá realizar trabalho (a normal não altera o módulo da velocidade do bloco). Então a força responsável pela variação da velocidade é a força peso. Temos que:

E se o bloco fosse abandonado na altura do plano inclinado (H = 12/sen30˚ = 6 m), qual seria o trabalho resultante?

Nesse caso a única força atuante é o peso. Então:

O que podemos concluir com isso? Algo notável! Não importa a trajetória do corpo, a variação da sua energia cinética e, consequentemente, o trabalho resultante, só dependem do desnível (altura) entre as suas posições inicial e final:

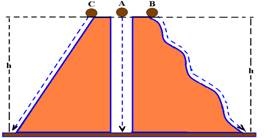
O trabalho resultante nas três trajetórias é o mesmo.

Esses sistemas sem atuação de forças dissipativas (atrito, resistência do ar) são chamados de sistema conservativos. A energia mecânica do corpo é constante durante a trajetória. Conforme o corpo ganha velocidade (energia cinética), perde energia potencial.

ENERGIA POTENCIAL DE UM CORPO DE MASSA M:

Vamos estudar ao longo do curso três tipos de energias potencias: gravitacional, elástica e elétrica. Quando estiver falando de um corpo de massa m sofrendo um desnível h, sofrerá uma variação de energia potencial gravitacional.

Vamos pegar o exemplo da situação anterior, dos corpos A, B e C caindo de uma altura h. A velocidade inicial dos corpos era zero. Então, inicialmente, suas energias mecânicas valiam:

Como é um sistema conservativo, a energia total se conserva, ou seja:

A energia potencial não tem um valor fixo. Não podemos calcular a energia potencial de um ponto, mas podemos medir a variação de energia potencial entre dois pontos! O que se faz nos exercícios é escolher um ponto para a energia potencial ser zero, e aí, achar a energia em outro ponto qualquer. Mas, de fato, o que calculamos é a sua variação.

Exemplo 3

Uma bolinha de massa 80 g é arremessada do solo e alcança uma altura de 5 m, em relação ao solo. Qual foi a sua variação de energia potencial gravitacional?

Resolução:

Como a energia mecânica é constante:

Usando Torricelli:

Com isso conseguimos descobrir a sua velocidade inicial:

ENERGIA POTENCIAL ELÁSTICA:

Quando um corpo está atado a uma mola/ elástico, pode sofrer uma diferença de energia potencial elástica. Vamos imaginar um objeto preso a uma mola encolhida, em uma superfície horizontal. Ao soltar a mola, ela começara a se esticar, tendendo a voltar para a posição de equilíbrio. Durante esse movimento oscilatório, o objeto sofre variações de velocidade, ou seja, a sua energia cinética muda o tempo todo. A energia cinética mudando, há realização de trabalho. A força que faz a velocidade mudar é a força elástica:

O problema é que, como a força elástica depende da deformação da mola, durante o movimento oscilatório, a força elástica muda a cada instante de tempo. Como fazer para medir o trabalho da força elástica?

Sabemos que, quando a mola estica sofrendo uma deformação x, a força elástica vale, em módulo, F = kx. Em módulo porque, de fato, se a mola for esticada para a direita, a força elástica apontará a para esquerda (basta soltá-la que veremos para onde a mola começará a se mover).  Façamos um gráfico F x x:

Basta calcularmos a área do gráfico F x x que obteremos o trabalho que uma força externa F realiza ao deformar a mola, ou ainda i.e., a energia potencial do sistema (energia potencial elástica). Então, pelo gráfico, temos que:

Assim temos que a variação de energia potencial elástica quando um elástico/mola é deformado de x vale:

Exemplo 4

Um bloco de massa m parte do repouso a uma altura h₀ em relação ao solo. Ao final do movimento irá colidir com uma mola de constante elástica k. Qual será a máxima deformação sofrida pela mola?

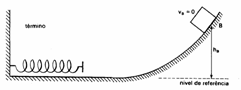
Resolução:

Como é um sistema conservativo, a energia mecânica se conserva, ou seja, conforme o bloco vai caindo, como a sua energia cinética vai aumentando, podemos inferir que sofre uma queda de energia potencial gravitacional. Como o bloco é parado pela mola, toda a sua energia cinética é reduzida a zero, indicando que o sistema massa-mola vai ganhando energia potencial elástica. Logo:

SISTEMAS NÃO CONSERVATIVOS:

Um homem descendo de paraquedas e um carro que freia são exemplos de sistemas que a energia mecânica diminui com o tempo, ou seja, há dissipação de energia. A força que o vento faz no paraquedas faz com que a velocidade de queda seja praticamente constante durante um certo período, ou seja, o homem perde energia potencial (está caindo), mas a cinética fica constante, portanto sofre perda de energia mecânica. No caso do carro, a força de atrito dissipa energia cinética do sistema.

No 1° caso, então, o trabalho do peso é igual, em módulo, ao trabalho da força do vento. Como não há variação de energia cinética, o trabalho total é nulo. Então:

Já no 2° caso, o trabalho da força de atrito é igual a variação de energia cinética do carro:

POTÊNCIA:

A grandeza potência (P) de um elemento (motor, por exemplo) mede o módulo da variação de sua energia cada intervalo de tempo.

Unidade de potência do S.I. : W (Watts).

Vamos estudar três tipos de potências: mecânica, térmica e elétrica.

POTÊNCIA MECÂNICA:

É a potência exercida por uma força motriz ou por uma força dissipativa em um corpo de massa m.

Exemplo 5

Um guindaste faz com que um corpo de massa 1,0 tonelada suba uma altura de 2,4 m em 2 minutos, com velocidade constante. Qual a potência do motor (ideal) do guindaste?

Resolução:

Como o corpo sobe com velocidade constante podemos inferir que o módulo do vetor peso é igual ao da força que o motor faz para levantá-lo (podemos pensar que há um cabo puxando-o, sendo assim, a tração seria a força motriz).

Então, a potência do motor será:

Repare que colocamos o intervalo de tempo em segundos (S.I.).

OBSERVAÇÃO

Para deslocamentos com velocidade constante, podemos ver que:

Perceba que potência também é uma grandeza escalar.

POTÊNCIA TÉRMICA:

É o calor liberado para um sistema em um intervalo de tempo.

A unidade do S.I. continua sendo W, que equivale a J/s. Porém, nesse tipo de assunto, é comum a unidade cal/s ou Kcal/s. Lembrando que 1 cal ≈ 4,18 J.

Exemplo 6

Um micro-ondas cuja potência vale 800 W é usado para aquecer 200 ml de água de 20˚C até 100˚C. Considerando que o sistema está no nível do mar, qual é o intervalo de tempo necessário para que a água sofra essa variação de temperatura?

Resolução:

Usamos 1 cal = 4 J e que o calor específico da água vale 1 cal/g˚C, ou seja, 4 J/g˚C. E sua densidade, 1 g/cm³.